Satyendra kr. Banjare

Differential Privacy

Aug 3, 2019
6 minute(s) read

“Privacy means people know what they’re signing up for, in plain language, and repeatedly. I believe people are smart. Some people want to share more than other people do. Ask them.” – Steve Jobs

As the world becomes more and more data driven, there is even more growing need of more secure systems to carefully meet the objectives of all the participants. There is a security and privacy need of every form, starting from a secure form response submission to data anonymization, there is work required in almost every area. In this blog we will discuss on a particular kind of attack called Linkage Attacks and the role of Differential Privacy methods to overcome them. Consequently we will try to extend the idealogy for differentially private programs.

Linkage Attacks

Linkage attacks are powerful privacy attacks on datasets that unveils identity of private and sensitive data about individuals (like name & address) by Linking few pieces of the data points, called Quasi-identifiers of one dataset with other datasets. This is just a statistical analysis method and thus one requires only dataset and potentially he/she can recover important data about people no matter how secure the system is.

One of most common example of such attacks is called Netflix Prize attack where a group of researchers were able to uniquely identify 87% of the US population whose movie ranking statistics were made avilable by Netflix. The combined the data with Census data to achieve this. More information can be found here Robust De-anonymization of Large Datasets (How to Break Anonymity of the Netflix Prize Dataset). There are several other examples that are brutul as well as funny, find more information over here CS5436 - Cornell.

There is a need to minimize privacy risks while maximizing data utility. One way to achieve this is to anoymize such Quasi-identifiers. Scientists have thus devised method of Differential privacy to help counter such attacks.

Differential Privacy

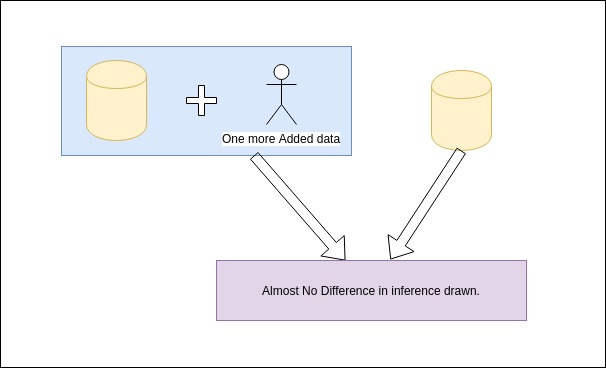
Differential Privacy is a probability based concept of guaranteeing the data anonymization upon its usage for analysis. This Data Anonymization is a security technique that is used to preserve sensitive data. It states that addition of one more data point to the dataset would be differntially insignificant to the net inference drawn. At times Differential Privacy is also understood as providing only specific information or rather incomplete information. This however may not be true. An anonymized dataset may contain all the information and still being differentially private.


The way this method works is by adding noise evenly to raw data in such a way that the overall probability distribution is not affected. The noise addition is done by using some randomization algorithms. These algorithms are consequently probabilistic and statistical. A very good discussion on this topic can be found here Privacy Book. The most common one being Laplacian Mechanisms and Gaussian Mechanisms can be looked in here Wiki-link. The development of these randomization algorithms is a good research topic.

More Formally, a system is called \(\epsilon\)-loss differentially private if, given two datasets A and B differing by only 1 data field, and R be randomization algorithm whose output is query result on the anonymized database.

\[ Pr(R(A)) \leq e^{\epsilon} * Pr(R(B)) \]

The anonymization achieved by usage of randomization algorithms can be generalized into two forms :

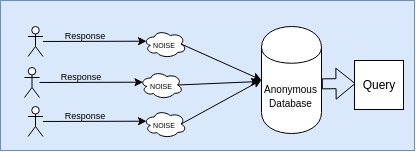
  • Local Privacy : The randomization is added to every response during the data generation only. The final database is anonymized. Finally this database is queried upon as wish to one’s need. There is supposed to be no backtrack to the true user’s response.
    • It is used by Google in uses this method to collect statics from Chrome.
    • RAPPOR is developed by google to implement local differential privacy.
    • Apple uses it to collect emoji usage data of iphone users.
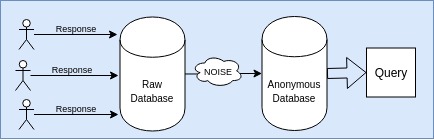
  • Global Privacy : The randomization is added to the whole raw database created. There is a possible space of data leaks in this case, if there is an access to the raw database.

Privay Budget (\( \epsilon \) )

There is a tradeoff performed between privacy and accuracy to meet a practical application. The most important caveats of differential privacy technology are :

  • The more information is asked, more the amount of randomization / noise is required.
  • Once an information is leaked, its public forever.

The measure of information leak which is thought of being insignificant is measured in terms of Privacy Budget. This is the limit of privacy loss that is allowed for a private database. Apple uses a privacy budget with \( \epsilon \) = 4 for lookup hints and \( \epsilon \) = 8 for QuickType. More information can be found here Differential Privacy - Apple.

Upon Adding more data fields, the privacy budget is assumed to be constant but however it is not the case always. The data anonymization is statistically better with more number of data fiels.

For a practical application, it may be understood as max number of queries allowed on a database. Now as number of queries is decided, the total dependence on the noise creation by randomization algorithms can be decided and hence the privacy loss limit be decided too.

It is studied mostly for large datasets. On small datasets this kind of privacy may not be achieved. Also its been proved that if used, this method is totally ineffective for small datasets.

Programming Language analysis of Differentially Privacy

DP is originally developed by the Cryptography community. People in programming language research community are actively combining ideas of formal analysis to prove the robustness of DP techniques. Research on development of Type system based approach is going on to create securely private randomizations by computer programs.

The recent works that I found out are :

Differential Privacy in Deep Learning

Application of DP is not only limited to Creating secure Databases. Some researchers at Google have implemented the idea of DP in Deep Learning to demonstrate that we can train deep neural networks with non-convex objectives, under a modest privacy budget, and at a manageable cost in software complexity, training efficiency, and model quality. Paper can be found here : Deep Learning with Differential Privacy - Ian GoodFellow.

References